第三章 决策树
决策树的数据必须是枚举类型的。或者说是整数。
信息增益和熵
符号xi的信息定义为:
l(xi) = -logp(xi)
熵的定义:
H = -Σ(p(xi)logp(xi))
熵的这种表示形式和逻辑回归很像。
对于数据集中标签的熵的计算方法,是:
1 计算概率p
1.1 p = label的数量/总的数据集的数量
2 计算熵
2.1 将所有的 -p*log(p) 相加求和
熵越高,表示混合的数据越多,可以在数据集中增加更多的分类,以便观察熵的变化。
分类
有了熵的定义,我们就知道所谓的分类就是使得熵不断的下降收敛,就是最好的分类。(因为熵越高,表示混合的数据越多;熵越低,表示逐渐在进行分类)
如何进行分类?所谓的分类就是将其中一个指定的特征量抽取出来,余下的组成数据集。例如: [[1, 0, 0], [1, 0, 2] [0, 1, 1]] 按照第一列抽取,就是[1, 1, 0]和剩下的[[0,0], [0, 2], [1, 1]], 指定特征量为0,那么结果就是[[0, 0], [0, 2]].按照第二列抽取,就是 [[1,0], [1, 2], [0, 1]] 指定特征量如果为1,就是[[1, 0], [1, 2]]
例如:
| 序号 | 不浮出水面是否可以生存 | 是否有脚蹼 | 是否属于鱼类 |
|---|---|---|---|
| 1 | 是 | 是 | 是 |
| 2 | 是 | 是 | 是 |
| 3 | 是 | 否 | 否 |
| 4 | 否 | 是 | 否 |
| 5 | 否 | 是 | 否 |
| 6 | 是 | 否 | 是 |
上面的表格,我们按照第二个特征量进行分类,按照value='是'进行分类的结果是:
Value='是'
| 序号 | 不浮出水面是否可以生存 | 是否属于鱼类 |
|---|---|---|
| 1 | 是 | 是 |
| 2 | 是 | 是 |
| 4 | 否 | 否 |
| 5 | 否 | 否 |
Value='否'
| 序号 | 不浮出水面是否可以生存 | 是否属于鱼类 |
|---|---|---|
| 3 | 是 | 否 |
| 6 | 是 | 是 |
注意:上面的结构表示,最后一列“是否属于鱼类”这个分类标签的位置永远没有改变,永远是最后一列。
熵的计算
对‘是’和‘否’的熵进行计算,找出熵最小的作
决策树的构建
在构建决策树中,看每层是否是相同的分类,如果是相同的分类,则不能继续划分,也就是叶子节点;如果不是相同的分类,可以继续划分。 看下里面的例子.
| 序号 | 不浮出水面是否可以生存 | 是否有脚蹼 | 是否属于鱼类 |
|---|---|---|---|
| 1 | 是 | 是 | 是 |
| 2 | 是 | 是 | 是 |
| 3 | 是 | 否 | 否 |
| 4 | 否 | 是 | 否 |
| 5 | 否 | 是 | 否 |
决策树的结果:
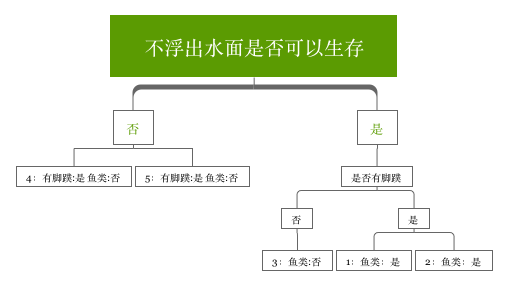
4,5组成的分类就是一个叶子节点,因为4和5的 label 都是一样的。都是 fish:否。