Lesson10 机器学习的优化方法
10-1 接下来尝试什么来改善机器学习的效果
当机器学习的效果不是那么理想的时候,有哪些方法可以尝试呢?
- 获取更多的训练集
- 尝试更小的特征集
- 增加特征集
- 尝试使用多项式, 例如 (x^2, x1x2, etc)
- 增加λ
- 减小λ
问题是,你可能花费了很长的时间在一个工作上,但是,效果依然不理想。那么,有可能你选择的方向就是错误的。那么,接下来通过机器学习诊断来让你更清楚接下来要做什么。
10-2 评估你的假设函数
当我们计算出来了J(θ)的正确表达式之后,通过评估的方式来知道当前算法时候好坏。评估的方法,步骤如下:
- 1 将测试集随机化
- 2 其中70%用作训练J(θ), 30%用作评估
对于线性回归来说,评估方法如下:
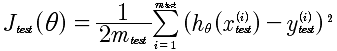
test下标表示测试集的意思
h(θ)是通过线性回归得到的函数
对于逻辑回归来说,评价方法如下:
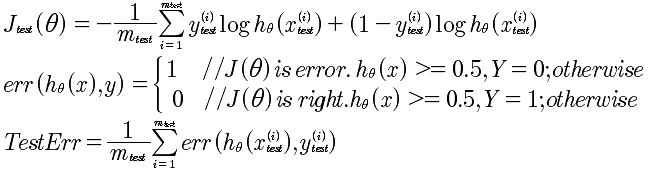
10-3 模型选择:训练集,交叉验证集,测试集
对于模型的选择,例如下面的线性回归方程,d(degree)表示x的幂,d=1,2,3...10
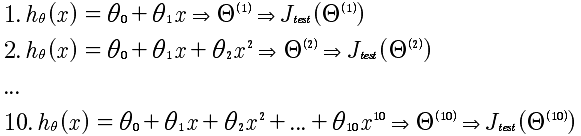
那么,现在通过对Err(J_test( Θ^5 ))效果最好,那么,我们选择了Θ^5 但这并非是正确的,因为现在变成了对测试集的最好的拟合。所以,需要重新进行数据集的划分。
分别是:训练集 占数据总量60%,交叉验证集占20%,测试集占20%。评估的方法,依然是寻找最小偏差。
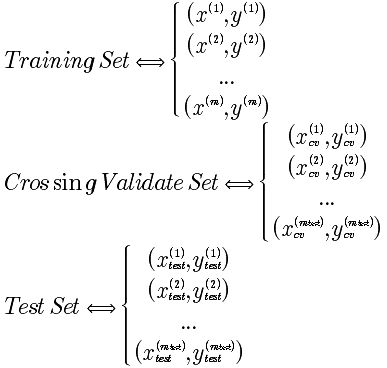
偏差公式:
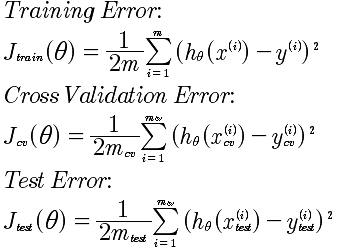
到现在,对机器学习其实有了一个总体框架的认识。就是寻找拟合,通过训练集,写出拟合标准就是J(θ),剩下的工作是寻找J(θ)的最小化的θ;因为在选择拟合函数h(θ)的时候,可能有多种选择,这没关系,把每一种情况计算出来,使用 J_cv(θ)来寻找最好的h(θ)模型.最后通过,测试集来进行测试。
对于模型的选择,就是根据某一个变量划分的模型,选择最好的那一个模型。事实上就是,绘制变量和J_test(θ)的曲线,来找到J_test(θ)最小的那一个。对于线性回归来说,是确定维度,那么维度d和J_test(θ)就构成了函数曲线。
10-4 偏差与方差
求解的假设函数,要么是偏差要么是方差大。这是针对训练集和测试集来说的。如果是偏差,说明是欠拟合,如果是误差大说明是过拟合。所以搞清楚这个问题,非常重要,给了我们一个指示器,进行优化。
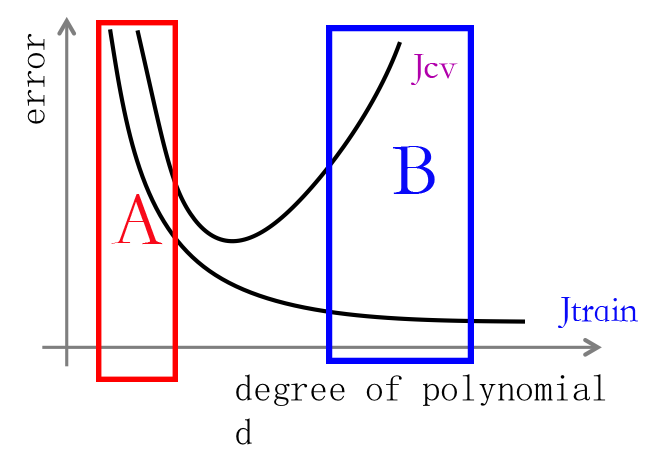
横坐标: d 表示多项式的最高次幂
纵坐标: 表示误差
我们看到,当d的取值很小的时候,对于训练集来说产生的误差比较高,同样对于验证集来说也很高,这是一种欠拟合的形态。对应A的区域。再看B的区域,因为d的取值很高,所以对于训练集来说能够很好的拟合,但是,对于验证集来说,却误差很大。这说明是过拟合。
欠拟合,偏差的定义如下:
1. J_train(θ) 很高
2. J_cv(θ) 约等于 J_train(θ)
过拟合,误差的定义如下:
1. J_train(θ) 很小
2. J_cv(θ) 远远大于 J_train(θ)
上面的图告诉我们如何来确定是高偏差还是高误差。然后,后面的优化再对症下药。因为每一个参数的调整,要么产生偏差猫么产生误差。
10-5 正规化
正规化可以有效的解决过拟合的问题。同样,正规化可以有效的处理偏差和方差的问题。看下,正规化的表达式。
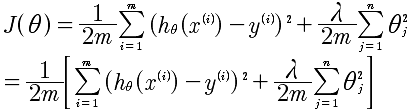
通过这个表达式,我们可以理解到,正则化是为了在选定的d的情况下的再次优化。是针对特定的d的细致优化。但是即使对于选定的d,依然可以进行再优化,那就是通过上面的正规化方法。通过对θ的惩罚来达到更加好的拟合。
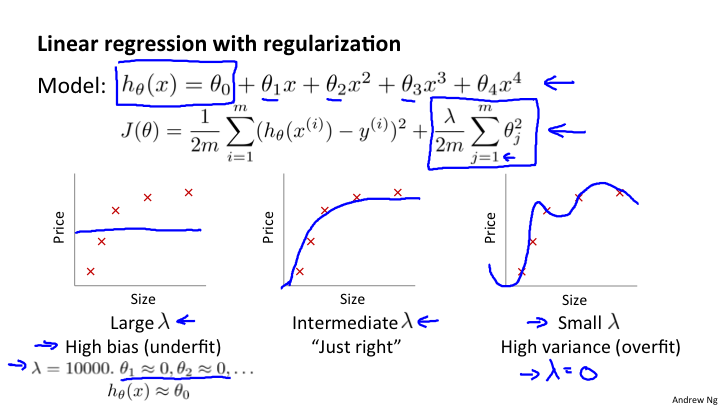
上面的图像展示了对于同一个d=4来说,选取不同的λ,可以产生不同的拟合。选择恰当的λ也可以实现正常的拟合。
那么对于误差公式来说:
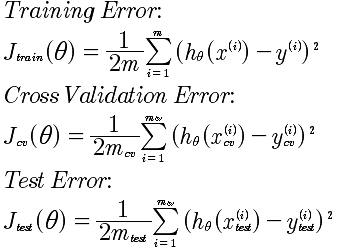
特别注意: 训练集误差是没有正规化表达式的。正规化表达式是中间的过程优化的计算思想,而对于误差的最终描述是没有这一项的,这一点要搞清楚。
之间的图像和变化关系又是什么样的呢?
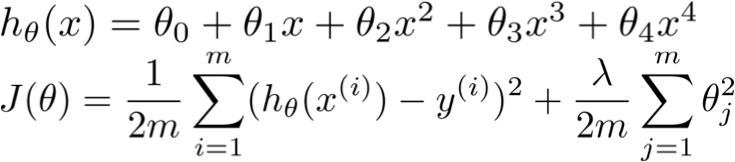
计算的过程如下表:
| λ取值 | 计算步骤1 | 计算步骤2 | 计算步骤3 |
|---|---|---|---|
| 0 | min(J(θ)) | 得出 θ^(1) | 得出 J_cv(θ) |
| 0.01 | min(J(θ)) | 得出 θ^(2) | 得出 J_cv(θ) |
| 0.02 | min(J(θ)) | 得出 θ^(3) | 得出 J_cv(θ) |
| 0.04 | min(J(θ)) | 得出 θ^(4) | 得出 J_cv(θ) |
| ... | min(J(θ)) | ... | 得出 J_cv(θ) |
| 10 | min(J(θ)) | 得出 θ^(10) | 得出 J_cv(θ) |
那么,从中选择最小的 J_cv(θ)的值,就是我们需要的θ取值。
通过上面的表格,通过图像来看就会更加直观。将J_train(θ)和J_cv(θ),两个误差函数进行绘制。
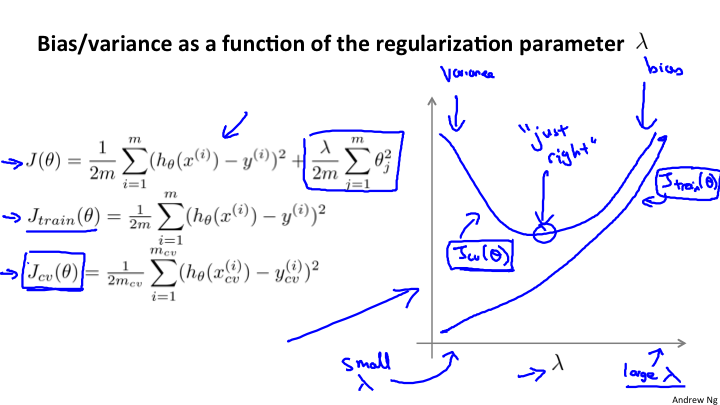
可以看到对于λ很小的时候,产生的开口很大,因为对于θ来说,没有惩罚,所以还是会产生高误差;而对于λ的增加,会对θ惩罚很大,最后会出现很接近。对于我们来说,选择中间的点是最合理的。
10-6 学习曲线
绘制学习曲线是非常有用的方法。能够检测你的学习算法,以及所处的问题是偏差还是方差问题。
高偏差(欠拟合)解释
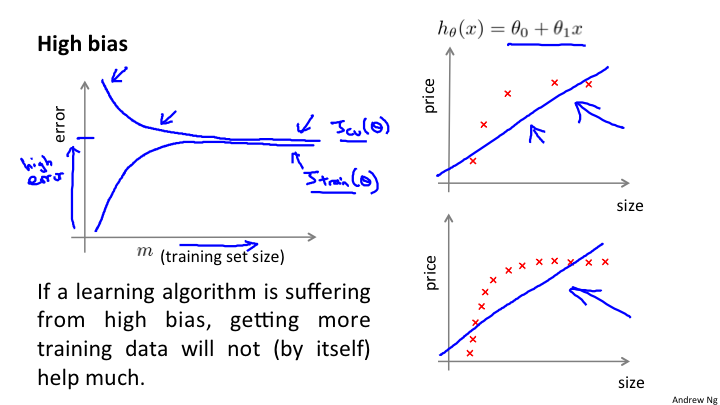
这张图是对高偏差的学习曲线的一个描述。坐标系描述,如下:
error:纵轴表示误差数值
m: 表示数据集个数。这一点需要注意,如果是训练集表示的训练集个数;而交叉验证集是使用的全体
学习曲线的解释:对于每一个训练集,训练出来的参数,应用到整个交叉验证集,计算出训练集误差;再应用到训练集,计算出训练误差。
对于图上的高偏差(欠拟合)的理解。对于J_train(θ)在数据量很小的时候,也就是m=1,2... 很小的时候,因为h(θ)能够对训练集数据很好的拟合,所以J_train(θ)就会很小;随着m的增加,会使得J_train(θ)的偏差会逐渐增大;但是,当m增加到一定的数量,因为欠拟合,所以J_train(θ)维持在一个较高的位置,但是不会再急速上升,而是平稳下来。
而对于 J_cv(θ)的理解是这样的。当数据量很小的时候,m=1,2,...的时候,因为验证集的数据很少,所以不会很好的与h(θ)拟合,就会产生较大偏差,也就是error(J_train(θ))会比较大;随着数据量的增加,逐渐的拟合度增加,误差值就会逐渐的变小;当数据量大到一定的程度的时候。J_cv(θ)和J_train(θ)就会很接近处于一致的位置。
这就是对于高偏差的解释。所以对于学习曲线来说,高偏差的特征是:
1 J\_train(θ)和J\_cv(θ)比较接近,而且处于较高位置
2 对于这样的情况来说,增加数据集是没有任何意义的
高误差(过拟合)解释

对于高误差(过拟合)的理解。对于J_train(θ)在数据量很小的时候,也就是m=1,2... 很小的时候,因为h(θ)能够对训练集数据很好的拟合,所以J_train(θ)就会很小;随着m的增加,会使得J_train(θ)的偏差会逐渐增大;对于这一点上与高偏差是基本一致的。
而对于 J_cv(θ)的理解是这样的。当数据量很小的时候,m=1,2,...的时候,因为验证集的数据很少,所以不会很好的与h(θ)拟合,就会产生较大偏差,也就是error(J_train(θ))会比较大;随着数据量的增加,逐渐的拟合度增加,误差值就会逐渐的变小;而当训练集和验证集的数据使用完的时候,对于J_train(θ)J_cv(θ)和J_train(θ)就会在一个位置保持很大的差距,也就是gap.
但是通过图像,可以看出,如果继续增加训练集和验证集的数据,二者会继续下降,所以增加数据集是有用的一个方法。
这就是对于高误差的解释。所以对于学习曲线来说,高误差的特征是:
1 J\_train(θ)和J\_cv(θ)之间的差距较大。
2 对于这样的情况来说,可以增加数据集来使得结果拟合的更好。
10-7 回顾和总结
最初提出的问题的解决方案如下:
| 序号 | 解决方案 | 适用的问题 |
|---|---|---|
| 1 | 获取更多的训练集 | 高误差(过拟合) |
| 2 | 尝试更小的特征集 | 高误差 (过拟合) |
| 3 | 增加特征集 | 高偏差(欠拟合) |
| 4 | 尝试使用多项式, 例如 (x^2, x1x2, etc) | 高偏差(欠拟合) |
| 5 | 增加λ | 高误差 (过拟合) |
| 6 | 减小λ | 高偏差(欠拟合) |
对于当前是高偏差还是高误差的判断,使用学习曲线来判断。
神经网络的优化
前面所描述的都是基于线性回归的描述,那么,基于神经网络的优化又是什么呢?面临着两个问题。
一、隐藏层数的选择。究竟是几层。这个问题的处理与多项式选择中的最高次幂是一样的。可以通过 J_cv(θ)的比较来得出最好的θ.
二、使用正规化来进行优化。一个大型的神经网络配置正规化修订,要比一个小型的神经网络更加准确。
可以通过正规化来进行过拟合的优化。