小结4-概率全息表

概率分布

对照表,各种分布，概率密度，分布函数，期望，以及相关的所有公式的全方位的总结。

序号	离散型随机变量分布	记号
1	0-1分布	--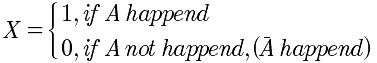
2	二项分布	X~B(n,p)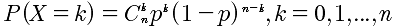
3	泊松分布	x~π(λ)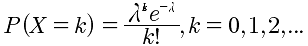
4	几何分布	X~Geom(p)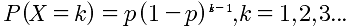

分布函数

离散型分布函数:

1 F(x)=P(X<=x)
2 P(a < X <=b) = P(X<=b) - P(X<=a) = F(b) - F(a)
3 P(a < X < b) = P(a< X <= b-0) = F(b) - F(a)
4 P(X=b) = P(X <= b) - P(X<b) = F(b) - F(b-0)
5 P(a< X < b) = P(a< X <= b) - P(X=b)

一般地，离散型随机变量的分布函数为阶梯函数，假设X的分布律为P(X=xk)=pk, k=1, 2,..., X的分布函数为 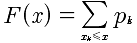,F(x)在x=xk(k=1,2,...)处有跳跃，跳跃值为pk=P(X=xk).

连续型随机变量X的分布函数F(x):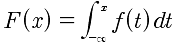，其中f(x)称为X的概率密度函数。

概率密度的性质:

f(x)>=0
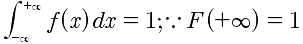
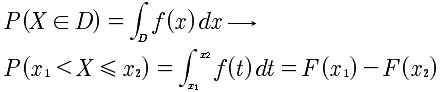
F'(x)=f(x)

概率密度典型分布函数:

序号	连续型随机变量概率密度	记号
1	均匀分布	X~U(a,b)
2	指数分布	X~E(λ)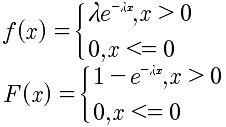
3	正态分布	X~N(μ,σ)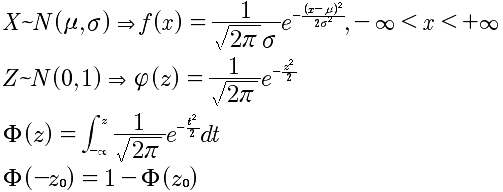

Y=g(x)的概率密度求解定理:

设随机变量X~fX(x),-∞<x<+∞, Y=g(X)，g'(x)>0或者g'(x)<0，则Y具有概率密度为:

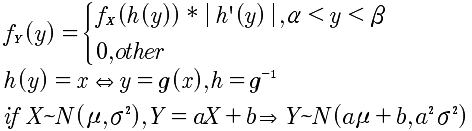
二元随机变量

离散型二元随机变量:

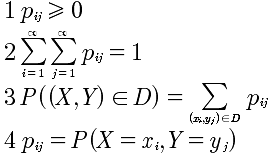
离散型二元随机变量边际分布率:

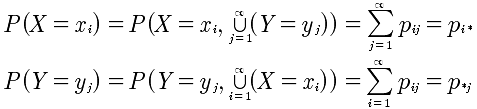
下面的表格很清楚的表达了二元随机变量的概率分布。

离散型二元随机变量条件分布律:

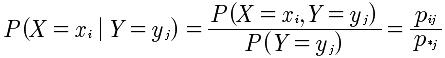
连续型二元随机变量:

联合分布函数:

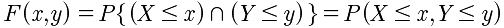
将X<=x,Y<=y看成是(x,y)的区域，就是这个区域内的所有概率相加.

边际分布函数.

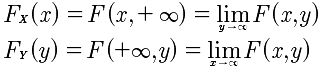
离散型条件分布函数:

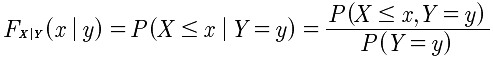
连续型条件分布函数:

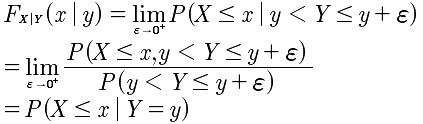
二元连续型随机变量

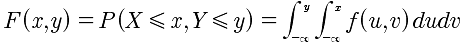
性质如下:

f(x,y) >= 0
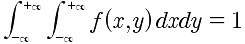
设D是xoy平面的区域，点(X,Y)落在D内的概率为:
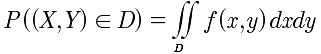
在f(x,y)的连续点(x,y)，有

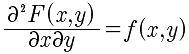
边际分布函数:

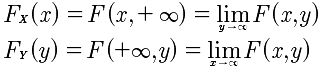
边际概率密度:

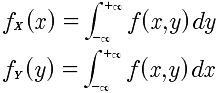
条件概率密度:

对于固定的y(注意是固定的y，也就是y等于某个常数),fY(y)>0,并且fY(y)连续，则在Y=y的条件下,X的条件概率是:

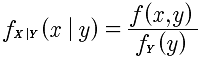
二元均匀分布

二元随机变量(X,Y)的概率密度在一个游街的区域D内是常数，其他地方为0，则称(X,Y)在D上服从均匀分布。设f(x,y)= 1/A (x,y)∈D 或者 f(x,y)=0, 其他.

二元正态分布

设二元随机变量(X,Y)的概率密度为:

边际概率密度:

条件概率密度:

二元随机变量的独立性

若P(X<=x, Y<=y)=P(X<=x)P(Y<=y)即F(x,y)=FX(x)FY(y)，则称X,Y相互独立。

离散型独立判断: 对一切i,j都有: P(X=xi,Y=yj)=P(X=xi)P(Y=yi)

连续型独立判断: 对于平面的点(x,y)，处处有f(x,y)=fX(x)fY(y)

二元正态随机变量(X,Y)，独立的充要条件是ρ=0.

多元随机变量独立定理:

设(X1,X2,...,Xm)与(Y1,Y2,...,Yn)相互独立,则有

Xi与Yj相互独立
h(x1,x2,..,xm)和g(y1,y2,...yn)是连续函数，则h与g相互独立。也就是说线性相关的也相互独立。

二元随机变量的函数分布

Z=X+Y的概率密度为:

正态分布的分布:

离散型随机变量的独立和分布

M=max(X,Y) 和 N=min(X,Y)的分布

数学期望

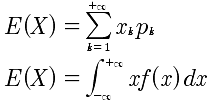
分布名称	期望
泊松分布 X~π(λ)	E(X)=λ
正态分布 X~N(μ,σ**2)	E(X) = μ
指数分布 X~E(λ)	E(X) = 1/λ
二项分布 X~B(n,p)	E(X) = np
几何分布 X~G(p)	E(X) = 1/p
均匀分布 X~U(a,b)	E(X) = (a+b)/2

随机变量函数的期望:

数学期望的性质

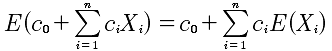
X,Y相互独立，有

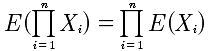
方差

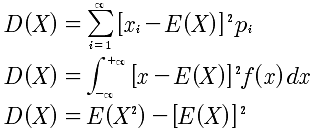
分布名称	期望	方差
泊松分布 X~π(λ)	E(X)=λ	D(X)=λ
正态分布 X~N(μ,σ**2)	E(X) = μ	D(X)=σ**2
指数分布 X~E(λ)	E(X) = 1/λ	D(X)=1/λ**2
二项分布 X~B(n,p)	E(X) = np	D(x)=np(1-p)
几何分布 X~G(p)	E(X) = 1/p
均匀分布 X~U(a,b)	E(X) = (a+b)/2	D(X)=(b-a)**2/12

性质:

正态分布的期望和方差:

随机变量标准化的过程: 特别注意：标准化的过程是将随机变量的量纲消除了。并且将均值变为0，方差变为1.

概率全息知识小结