Week2
第五讲 等可能概型
古典概率论,要求如下两点:
- 样本空间S中的样本点,必须是有限的
- 每个元素出现的概率,必须是等可能的
所以对于事件A来说,A中所包含的样本点除以S的样本点数,就是概率.
P(A)= 中所包含的样本点 / S的样本点数
问题: 如果有N个球,其中a个白球,b=N-a个黄球,采用不放回抽样取n个球(n ≤N),记Ak={恰好取到k个白球}(k≤a),求P(Ak)?
1 计算S. 取出n个球,那么S的样本点数是 C(N,n)
2 计算Ak包含的样本点数。Ak的含义是n个球,其中k个白球,n-k个黄球。那么:C(a,k)*C(b,n-k).
3 P(Ak) = C(a,k)*C(b,n-k)/C(N,n)
第六讲 条件概率
P(B|A)表示A发生的条件下B发生的概率。这里可以理解为,在A是一个全新的样本空间,只是A的概率不是1.由此可以看出对于任意概率,事实都是P(A|S)在全样本空间下的条件概率。条件概率公式:
P(B|A) = P(AB)/P(A);
当A=S的时候,P(B|S)=P(BS)/P(S)=P(B)
注意区别P(B|A)和P(AB)的含义。P(AB)的描述是AB同时发生;而P(B|A)是A发生的情况下B的概率。通过公式知道 P(B|A) > P(AB). 都是AB的概率,但是样本空间不同。
条件概率满足概率的所有性质。
计算用到的推导式:
P(AB) = P(A) * P(B|A)
心得体会:条件概率,是改变了样本空间,这一点理解才是条件概率的根本,不是文字的理解。所以针对取两次球的问题,A1,A2, P(A1)*P(A2|A1) 这种条件概率的表述,是因为取走了A1之后,样本空间改变了。
第七讲 全概率公式和贝叶斯
一袋中有a个白球,b个黄球,记a+b=n.设每次摸到各球的概率相等,每次从袋中摸一球, 不放回地摸n次.则第k次摸到白球的概率均为a/n.现在用另一种方法计算第2次取到白球的概率.
解:
设Ai表示第i次取到白球,i=1,2
P(A2)=P(A1A2 ∪ ~A1A2) = P(A1A2)+P(~A1A2)
P(A1A2) = P(A1)*P(A2|A1) = a/n * (a-1)/(n-1) = a(a-1)/n*(n-1)
P(~A1A2) = P(~A1) * P(A2|~A1) = b/n * a/(n-1) = ab/n*(n-1)
P(A2) = (a(a-1)+ab) / n*(n-1) = a(a+b-1)/n*(n-1)=a(n-1)/n*(n-1)=a/n
全概率定义:称B1,B2,...,Bn为S的一个划分,若
- 不漏。即:B1∪B2∪...∪Bn = S
- 不重。即:BiBj = ∅,i != j,任意两个不相容.
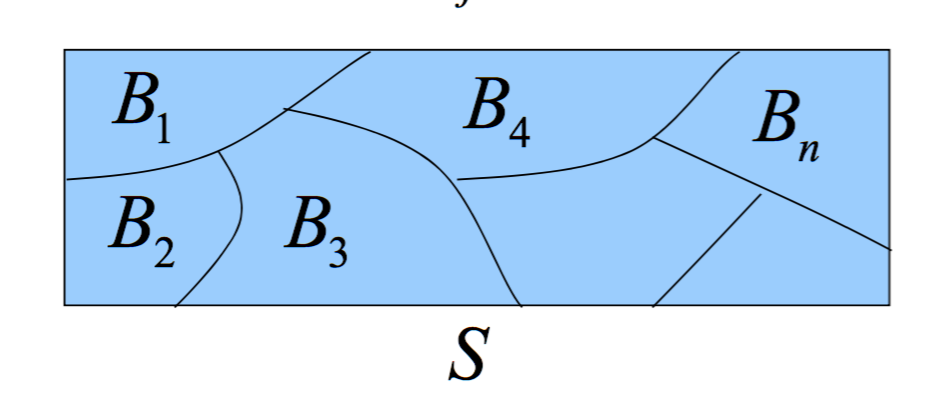
全概率公式:
P(A) = ΣP(Bj)*P(A|Bj), 其中Bj是第j个划分,Bj满足不漏和不重两个重要性质.
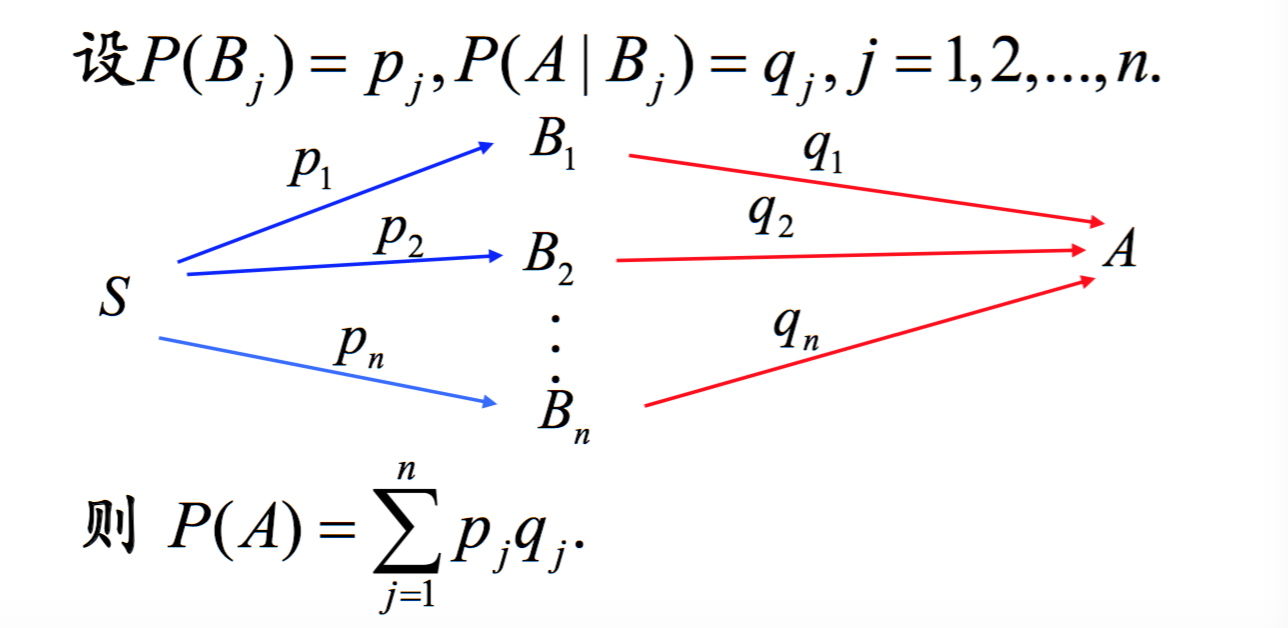
这样理解全概率,S被划分了n个部分,用B来表示,每一个部分有自己的概率,用p来表示,A相对于每一个区域的概率是q. 所以P(A) = pq. 注意,P(A)的概率的样本空间是S.所以在使用全概率的时候,重要的就是B的划分。
已知区域B的概率p,求A的概率q,被称作先验概率。那么能否,知道A的概率q,求B的概率呢?这就是后验概率,也就是贝叶斯公式。
P(Bi|A) = P(ABi)/P(A) = P(Bi)*P(A|Bi)/P(A) = pi*qi/Σpq
贝叶斯的语言描述是,A发生时,每个划分的概率。
在机器学习中的应用,是这样的。每一个划分,Bi其实就是一个分类,所以对于机器学习来说,就是通过给定的样本,对于不同特征的发生情况下,求Bi的过程。形式化描述,如下:
样本每条记录有n个特征值,分别记做 X={x1, x2,...,xn},其中每一个特征值,有ki种取值(例如x1有k1=3种取值,就是x1有3种取值)。那么,对于任意一种所有特征取值的排列组成的集合称作Aj(一共最多有k1*k2*...kn个A, j∈[1, k1*k2*...*kn]), B表示所有分类,一共包含B1,B2,...Bm个分类。
那么,Aj属于哪一个分类呢?
训练算法:
计算P(Bi|Aj)的概率,i从1到m, 取最大值, 就是Aj的分类。解释,P(Bi|A)的含义就是Aj出现时候,Bi出现的概率,那么,显然Bi最大值,就是Aj决定的分类。这里隐含了,Bi∩Bj=∅,B1∪B2...∪Bm = S.
预测算法:
给定一条记录,将该条记录中的所有特征值比对Aj中的那种组合,就是相应的分类。
具体举例来说。
样本有3个特征量,X={x1, x2, x3}, x1的取值有2种(w,t),x2有3种(0,1,2),x3有2种(p,q), k1=2, k2=3,k3=2. A的集合就是所有组合,一共有:232=12个元素. A={(w,0,p),(w,1,p),(w,0,q)....}. 假设一共有3个分类。B={B1,B2,B3}.
训练的样本数据如下:
| x1 | x2 | x3 | B |
|---|---|---|---|
| w | 0 | p | b |
| w | 1 | q | c |
| ... | ... | ... | ... |
| t | 1 | p | a |
算法伪代码:
训练算法:
1. 提取x1,x2,x3所有特征值的值
2. 将x1,x2,x3中分别取出一个元素,组成三元组,作为一个事件,事件的集合记做A
3. 计算A中,每一个元素的概率P(Aj)
3.1 P(Aj)计算:找到所有Aj的行/总的样本数
4. 取出B中的标签种类,记做集合B
5. 计算B中每一个标签种类的概率
5.1 计算Bi的行数/总的样本数
6. 计算所有的条件概率概率P(Aj|Bi), i取[1, size(Bi)],j取[1, size(Aj)]
7. 计算分类的条件概率 max(P(Bi|A1)), i取[1,size(Bi)],当i=I1时,max(P(Bi|Aj))=P(BI1|A1); I1就是A1的分类。同理,计算A2,...,Ak => I2, ..., Ik
8. I1, I2, ...,Ik 就是分类
预测算法:
1. 给定一个预测样本x,匹配在A中的位置,是xk, 那么分类就是Ixk.
心得体会:全概率,条件概率问题绘制区域分布图,是一种最好的解决方案。
tips
P(A-AB) = P(A) - P(AB). P(A) = P(A~B ∪ AB) = P(A~B) + P(AB) - 0 = P(A-AB) + P(AB)
第八讲 事件的独立性
P(AB) = P(A)P(B)称作A和B是相互独立的事件。
(1) P(AB) = P(A)P(B)
(2) P(AC) = P(A)P(C)
(3) P(BC) = P(B)P(C)
(4) P(ABC) = P(A)P(B)P(C)
其中: (1) (2) (3)成立,称作A B C两两独立;而 (1) (2) (3) (4)成立,都成立才称作相互独立。
考虑A B独立和A B相容。如果A B不相容,说明 A∩B=∅,显然 P(AB)=0, 而 P(A),P(B)>0,所以不成立。也就是说如果A B不相容,那么A B一定不独立。为什么会有这样的结论? 这样理解,假设S=A∪B,并且 A∩B=∅,则当A发生的时候,B的概率就是~A.所以二者是绝对关联的,所以不可能是独立的事件。所以只有A∩B != ∅, 才能去讨论独立的问题。
在实际问题中,往往不是通过公式来计算是否独立的,而是根据实际情况的特点来确定是否独立的。然后使用概率的乘积来简化计算。所以对于现在来说,计算P(AB)优先考虑是否是独立的再计算. 这样的方式对并集的概率也提供了支撑。
P(A∪B) = P(A) + P(B) - P(AB) = P(A) + P(B) - P(A)P(B)